Some Thoughts on the Powers of 10

A while back, I assigned a puzzle about terminating and repeating decimals.

As part of working on this puzzle, this led me down the road of thinking about 1/2, 1/4, 1/8, 1/16, etc.

1/2 = 0.5

1/4 = 0.25

1/8 = 0.125

These fraction/decimals equivalents I already knew.

I then worked on 1/16. (I did it by doing long division, rather than using a calculator because I wanted to get a feel for this fraction.) It worked out to 0.0625. I started to notice that the number of digits in the decimal goes up by 1 each time.

1/2 has 1 digit after the decimal point. 1/4 has 2 digits after the decimal point, 1/8 has 3 digits, and 1/16 has 4 digits.

This links back to an idea that Claire, Rowan, and Sage had. They landed on the idea that a terminating decimal comes about because the denominator of the associated fraction goes evenly into 10, 100, 1000, etc.

I noticed:

1/2 terminates because 2 goes evenly into 10.

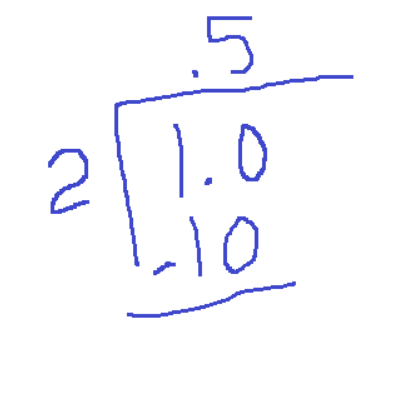
1/4 terminates because 4 goes evenly into 100.

1/8 terminates because 8 goes evenly into 1000.

1/16 terminates because 16 goes evenly into 10,000.

You start to see the pattern here....

I was very struck by the fact that 16 would go into 10,000 evenly. Now, of course, in some ways this is obvious:

10 = 5*2

100 = (5*5)*(2*2)

1000 = (5*5*5)*(2*2*2)

10,000 = (5*5*5*5)*(2*2*2*2)

So of course, 16 goes evenly into 10,000 because 10,000 = (5*5*5*5)*(2*2*2*2) = 625 * 16.

I was struck by this fact (that 16 goes into 10,000 evenly) because I hadn't thought about the "two-ness" of the powers of 10.

When I think of powers of 10, I think I have more often seen their "five-ness" or their "ten-ness."

For example, if someone asked me to name some factors of 10,000, I would say, "10, 100, 1000, or 2500." Before this activity, my mind did not jump to 16 as being one of its factors. Now, I know that 16 goes evenly into 10,000, 32 goes evenly into 100,000, and 64 goes evenly into 1,000,000, and so on.

This is not earth shattering by any means, but it was a fun discovery and a new way of looking at an old topic.